Ikosaedri
8.1.2021
Olen lukenut viime aikoina jonkin verran molekyylibiologisista aiheista Wikipediassa, ja teki mieli askarrella paperinen ikosaedri, saman muotoinen kuin monen viiruksen kapsidi. Paperisia kuutioita on tullut askarreltua pitkin peruskoulua ja joskus tylsistyneenä työelämässä, ja kuutio on varsin helppo muoto tasaisine 90-asteisine kulmineen. Rakensin kerran myös paperisen tetraedrin; se oli vähän haastavampi, sillä sen tiukat kulmat tekivät sivujen yhteen liimaamisen hankalaksi.
Ikosaedri koostuu kahdestakymmenestä kolmiosta. Itse aina näen ikosaedrin siten, että sen yläosa on viisikulmainen pyramidi, sen alaosa on toinen, ja molemmista pyramideista erittyy kolmiomaiset sormet, jotka menevät limittäin toisen puoliskon sormien kanssa.
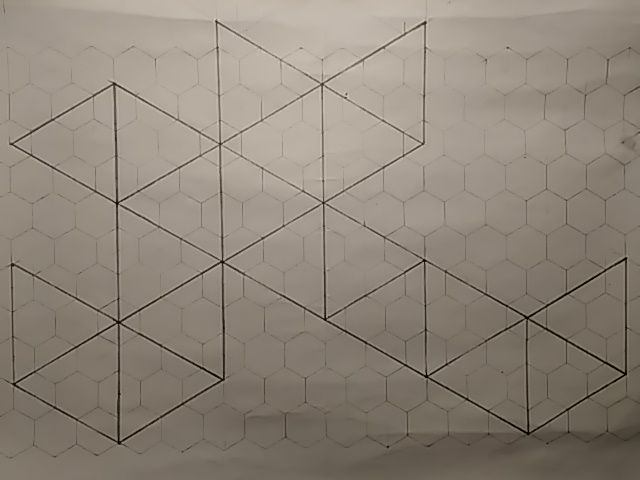
Olen ennestään tulostanut kuusikulmioisen ruudukon jotakin muuta varten. Koska tarvitsen jokaisen kuusikulmion keskipisteen, piirrän ruudukkoon lisäviivoja. Sain täten kolmioruudukon.
Kolmioruudukon avulla sain piirrettyä ikosaedrin verkon: 20 yhteenliitettyä kolmiota. Verkkoja on monia, ja tässä on vain yksi, eikä tämä ole edes kovin mieluisa; rajoitteina oli, että kolmioiden piti mahtua A4-paperille, sekä välttää yhdelle reunalle ilmestynyttä tahraa, mutta leikkaaminen ja liimaaminen hankaloitui jonkin verran. Paremmalla suunnittelulla olisi saatu helpompi sommitelma.
Väritin sitten kolmioiden sisällä olevat heksat. Käytin yhdeksää eri puuvärikynää. Tietysti jotkut heksat ylettyvät kahden tai kolmen kolmion yli. Reunoille jäi puolikkaita heksoja, joskus vielä pienempiäkin heksojen osia, jotka eivät täsmänneet toisen heksan puolikkaan kanssa kun ikosaedri kootaan; kolmioruudukko olisi ollut kaikin puolin parempi. Värittäessäni käytin aina sitä sääntöä että väri ei saa olla itsensä vieressä, edes koottunakaan. Yritin käyttää sitä sääntöä, että värin olisi oltava ainakin kahden mutta enintään kolmen heksan päässä toisesta samanvärisestä heksasta, mutten pystynyt noudattamaan tätä sääntöä; minulla on mututuntuma, että yhdeksällä värillä tämän säännön noudattaminen on mahdotonta, mutten ole todistanut sitä. Yritin myös värittää mahdollisimman pitkiä ketjuja sekä lämpimiä värejä (punainen, oranssi, keltainen, pinkki) että kylmiä värejä (tummansininen, vaaleansininen, violetti, tummanvihreä, vaaleanvihreä), mutta ketjut menivät ennemmin tai myöhemmin rikki. Uskon, että suunnittelulla kahden rikkoutumattoman ketjun värittäminen olisi mahdollista: ne menisivät limittäin, spiraalimaisesti.

Sitten leikkasin ylimääräisen paperin pois verkon ympäriltä, jättäen pienet läpät kasaan liimaamista varten. Tämä verkko ei ollut konveksi, joten leikkaaminen hankaloitui. Toisaalta liimattavia reunoja on vain 11, eli suunnilleen kolmasosa ikosaedrin 30 reunasta; en tiedä, onko kaikilla verkoilla 11 liimattavaa reunaa. Uskon, että joillakin voi olla enemmän, en tiedä voiko millään olla vähemmän, mutten yllättyisi todistuksista suuntaan tai toiseen.
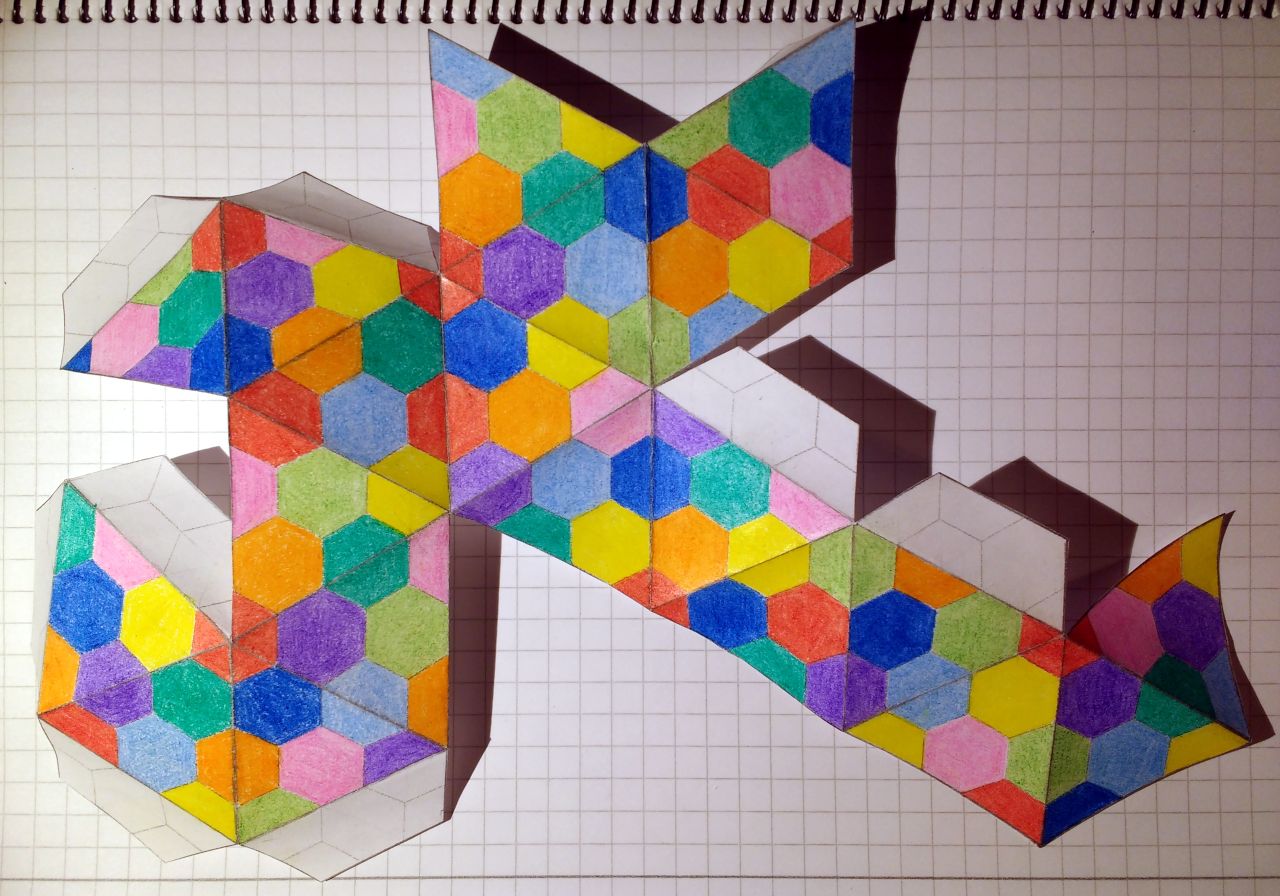
Sitten liimasin sivut yhteen. Viimeiset sivut olivat kaikista hankalimpia. Leikkaus- ja liimaustarkkuus oli amatöörimäistä. Mikään ei tietenkään voi olla matemaattisen tarkkaa, mutta kokemuksella ja osaamisella oltaisiin saatu siistimpi lopputulos. Milli sinne tai tänne leikkauksessa tai nuuttauksessa tarkoittaa muutaman asteen heittoa, jolloin teoreettisesti vierekkäisiksi tulevat väriheksat eivät enää ole vierekkäin, ja virheet kasvavat.
Lopputuloksesta tuli kuitenkin ihan kiva :)

Seuraavaksi se kuudesta muusta kuvakulmasta, jotta kaikki tahkot näkyvät.






Tahkojen numeroinnista
Tahkot voi numeroida mielivaltaisesti. 20-sivuisessa nopassa, d20:ssä, käytetään seuraavanlaista numerointia:

Tämän nimenomaisen ikosaedrin tahkojen numerointiin käytän tätä yksinkertaisempaa numerointia:

Tämän verkon voi tulkita binääripuuna, jossa jokaisella solmulla eli tahkolla (paitsi tietysti juurella ja viimeisillä) on yksi vanhempi sekä vasen tai oikea lapsi (tai molemmat), jotka määritellään vasemman- tai oikeanpuoleisen reunan perusteella, kun kolmio käännetään siten, että vanhempi on ylhäällä. Lisäksi jokaiselle yksilapsiselle kolmiolle voidaan merkitä linkki toiseen kolmioon, joka merkitsee liimattavaa reunaa.
Tässä alla kirjoitan auki oman ikosaedrinumerointini puun puumuodossa, käyttäen [n]-merkintää tarkoittamaan liimattavaa reunaa.
1
/ \
[10] 2
/ \
3 [20]
/ \
/-----------------/ 4
/ / \
11 5 \-------\
/ \ / \ \
[15] 12 [12] 6 16
/ \ / \ / \
[5] 13 7 [17] 20 17
/ \ / \ / \ / \
[7] 14 [13] 8 [19] [2] [6] 18
/ \ / \ / \
[9] 15 9 [18] [8] [19]
/ \ / \
[1] [11] [14] 10
/ \
[1] 19
/ \
[20] [18]
S-lausekkeena ilmaistuna puu on seuraavanlainen:
(1 ([10]) (2 (3 (11 ([15]) (12 ([5]) (13 ([7]) (14 ([9]) (15 ([1]) ([11])))))) (4 (5 ([12]) (6 (7 ([13]) (8 (9 ([14]) (10 ([1]) (19 ([20]) ([18])))) ([18]))) ([17]))) (16 (20 ([19]) ([2])) (17 ([6]) (18 ([8]) ([19])))))) ([20]))).
Visualisoi esimerkiksi tällä työkalulla.

Bitit vierusmatriisia varten: 01000000010000100000-10100000000000000001-01010000001000000000-00101000000000010000-00010100000100000000-00001010000000001000-00000101000010000000-00000010100000000100-00000001010001000000-10000000100000000010-00100000000100100000-00001000001010000000-00000010000101000000-00000000100010100000-10000000001001000000-00010000000000001001-00000100000000010100-00000001000000001010-00000000010000000101-01000000000000010010.

Tiilitettynä vierusmatriisi näyttää minusta ruumisarkuilta.