Koordinaattien tarkkuus

Nimenomaisesti kartta- tai GPS-koordinaattien tarkkuus.

xkcd:llä on tämä yksi comicci, numero 2170, julkaistu 1.7.2021, jonka aiheena on GPS-koordi­naattien tarkkuus:

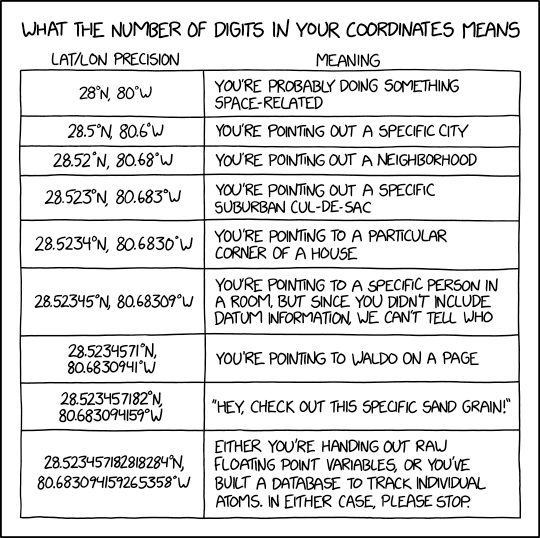
Sen viestinä on, että yli neljän tai viiden desimaalin antaminen ei ole mielekästä, sillä liian monesta desimaalista saa vain näennäistä tarkkuutta, kun mittaus­laite tuskin edes yltää niin tarkkoihin lukemiin, eivätkä Yhdys­valtain avaruus­voimat (on siinäkin ilmaisu :D) edes sallisi siviili­laitteistolta niin tarkkoja GPS-lukemia.

Mutta tämä sai miettimään: sarjakuva kertoo vain asteen desimaaleista, mutta entä jos paikkatiedon lähte käyttää aste-minuutti-sekunti -ilmaisua? Lisäksi, tämä koordi­naa­tis­tohan on ruudukko, mutta maapallo on suurin piirtein pallomainen, joten miten tarkkuus muuttuu kauemmas päivän­tasaajalta mentäessä? Olemmehan täällä Suomessa jo varsin pohjoisessa.

Tässä pieni Javascript-härpäke, joka laskee leveysasteen viivan liki­määräisen pituuden päivän­tasaajalta navalle, olettaen maapallon olevan sileä ellipsoidi. Eli tämä laskee sen ympyrän pituuden, joka saadaan, jos yritetään matkustaa sileän maapallon pintaa pitkin siten, että leveysaste pysyy vakiona, ja käydään läpi kaikki pituus­asteet.

Koko laskin käyttää WGS84:n lukuja maapallon muodolle sekä leveys­asteen koon laskemiseksi.

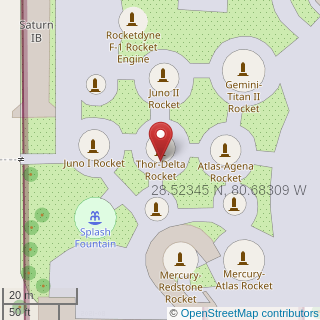
Yhden leveys­asteen­kaan pituus ei ole vakio, mutta ei vaihtele niin suuresti, ollen aina liki­määrin 111 km. Laskurin laskema leveys­asteen suuruus ei siis ole pituus­aste­sidon­nainen, vaan jos esimer­kiksi otetaan leveys­asteeksi 65° N, niin etäisyys 64.5° N–65.5° N on aidosti suunnilleen kilometrin pidempi kuin etäisyys 4.5° N–5.5° N.

Matikka löytyy myös Wikipediasta (sieltä sen löysin alun perinkin), mutta kun tätä aina välillä tarvitsee, ja kun en heti jaksa ruveta tulkitsemaan kreikkalaisia symboleita, kirjoitan tämän algoritmisesti auki:

radius_eq  = 6378.1370
radius_pol = 6356.7523
ecc_2 = (radius_eq^2 - radius_pol^2) / (radius_eq^2)
# Tai vaihtoehtoisesti: ecc_2 = 0.0818192^2
# Oletetaan, että trigonometriset funktiot käyttävät radiaaneja.
latitude = (syöte)
lat_rad = latitude * (180 / pii)
# Eli: lat_rad = latitude * 0.017453293
numerator = 2 * pii * radius_eq * cos(lat_rad)
denominator = sqrt(1 - ecc_2 * sin(lat_rad)^2)
parallel_of_latitude = numerator / denominator
degree_of_longitude = parallel_of_latitude / 360
degree_of_latitude = 111.132954 - 0.559822 * cos(2*lat_rad) + 0.001175 * cos(4*lat_rad)

Jos olettaa maapallon olevan täydellinen litistymätön pallo, on lasku paljon helpompi: 40075 * cos(latitudi * (pii/180)).

Anyway, palatakseni aiempaan pointtiini: kuinka monta desimaali­piste on liian monta?

xkcd:n numerossa 2170 esitetään yksi toisensa jälkeen tarkempia koordinaatteja. 28°N, 80°W osoittaa suurin piirtein Floridaan; 28.000°N, 80.000°W on noin 50 km itään Melbournen kaupungista, Atlantin valtameressä. Yhdellä desimaalilla (28.5°N, 80.6°W) osoitetaan tarkalleen Cape Canaveral Space Force Stationin ja Merrit Islandin väliseen vesistöön, mutta karkeammin ymmärrämme kyseessä olevan Cape Canaveralin avaruus­kompleksi. Kahdella desimaalilla tiedämme jo olevamme Kennedyn avaruus­keskuksen vieras­keskuksessa. Viidellä desimaalilla, 28.52345°N, 80.68309°W, osoitetaan tarkalleen näytillä olevaan Thor-Delta -rakettiin, ja lisädesimaalit ovat jo turhia.

28.5°-leveysasteella yksi leveysaste on 110 828 metriä pitkä, ja yksi pituusaste on 97 904 metriä. Ensimmäinen desimaali antaa siis 11 km × 10 km -kokoisen alueen, ja toinen desimaali osoittaa tiettyyn neliökilometriin. Kolme desimaalia ilmaisevat paikan hehtaarin tarkkudella, ja Helsingin korkeudella jo puolen hehtaarin: pituussuuntaista tarkkuutta on 50 metriä, Nuorgamin korkeudella 38 metriä. Neljä desimaalia ilmaisee paikan jo 10 metrin tarkkuudella, ja viidellä desimaalilla metrin tarkkuudella, jonka arvelisi olevan riittävän tarkkaa.

Mutta entä minuutteina ja sekunteina? Asteessa on 60 minuuttia, joissa jokaisessa on 60 sekuntia, eli sekunti on 3600. osa asteesta. Tämä on hieman karkeampi mitta kuin 4 desimaalipistettä, muttei kovin paljoa tarkempi. Sekunnin kymmenesosa, yhdellä desimaalilla, on suunnilleen yhtä tarkka kuin asteen 5. desimaali, kun sen pyöristää olemaan neljällä jaollinen. Päätelmäni siis on, että asteen kymmenystä tarkempi paikkatieto on ylitarkka.